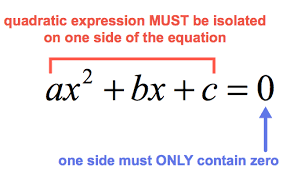Everything You Need To Know About Quadratic Equations
While quadratic equations may seem complicated, this article breaks down the steps involved in solving them and then explains how to use a graphing calculator so that you can begin solving them yourself.
What is a Quadratic Equation?
A quadratic equation is a mathematical equation in two variables that can be written as ax2+ bx + c = 0.
The most common type of quadratic equation is the equation y = x2. In this equation, y is the variable and x is the independent variable. The other type of quadratic equation is the equation ax2 + bx + c = 0, where a and b are constants.
In general, solving a quadratic equation requires solving for both the x-axis and y-axis values. However, there are a few cases where only one of these values needs to be solved.
For example, if y = –x2, then only the y-value needs to be solved. Additionally, Solutions to Quadratic Equations: The Basics shows how to solve a quadratic equation in two variables using Quadratic Formula and Complex Numbers.
Methods Solve Quadratic Equations:
There are three methods which can be used to solve quadratic equations: factoring, using square roots, and completing the square. In order to use any of these methods, however, it is first necessary to determine whether or not the equation has real solutions.
This can be done by checking to see if there are two distinct roots (or solutions) separated by integers; if there are no integral solutions then it is likely that either there is no solution or else one root is imaginary.
-Factoring Method:
The factoring method involves breaking down (factoring) both sides of the quadratic equation into polynomials and cancelling out like terms until only one term remains on each side.
Once this has been done, solving for x becomes simply a matter of rearranging algebraically until an answer can be found.
-Square Roots Method:
The square roots method uses radical notation to find all possible values for x which make the left hand side equal to zero.
It should be noted that this process will only work if coefficients “a” and “b” are positive numbers. If they are negative numbers then radicals cannot be taken and another method must be used instead (such as completing the square).
-Completing the Square Method:
The completing the square method is similar in principle square roots method; however it can be applied when coefficients “a “and “b” are either positive or negative numbers. This method works by transforming quadratic that are more simplified than using basic algebraic operations.
How to Graph a Quadratic Equation
If you’ve ever been stuck trying to solve a quadratic equation, Quadratic Calculator will help you graph the equation and get to the solution.
Start by writing the equation on a piece of paper and lining up the x-axis and y-axis. In order to graph the equation properly, it’s important to know its order: y2 – 4x + 8 = 0.
Now, begin drawing the line that corresponds to y2 – 4x + 8 = 0 on your graph. Note that this line will intersect the x-axis at two points: (0, -4) and (4, 8). These two points are called the solutions to the equation.
To find the second solution, move your cursor over (4, 8) and click. This will bring up a new window with information about the point. In this window, you’ll see that x = 4 and y = 8. Hence, the second solution is (4, 8).
How to Solve Quadratic Equations?
Now that we know what quadratic equations are and how to use the Quadratic Formula, let’s take a look at how to actually solve them manually or with the help of Quadratic Calculator. There are four basic steps involved:
- Factorize the equation
- Take out the Square Root
- Apply the Quadratic Formula
- Check your answer
The following examples will illustrate each step in more detail. Let’s start with an easy one…
Example 1: Solve 5x2+ 7x = 0
Step 1: Factorize 5x^2 + 7x = 0 into two brackets which each contain one factor of x: (5x+7) (x-0)
Step 2: Take out the Square Root √ (5x+7)(x-0) = ±√5x±7
Step 3: Apply The Quadratic Formula ax²+bx+c=0 →a=-7 b=5 c=0
Plugging these values into The Quadratic Formula gives us two answers: – √5×5±√7×(-1)=3±4 or -3±4
Solution set: {3,-3} So there are two solutions for this equation, 3 and -3 .
Checking these solutions against our original equation confirms that they work correctly.
Quadratic equations are a type of algebraic equation that can be solved using the Quadratic Calculator. There are three ways to solve quadratic equations: graphing, factoring, and using the quadratic formula. The solutions to a quadratic equation will always be real numbers.
When solving a quadratic equation, it is important to check the discriminant to determine what kind of solutions you will have. It can be used in many different applications, including physics and engineering.